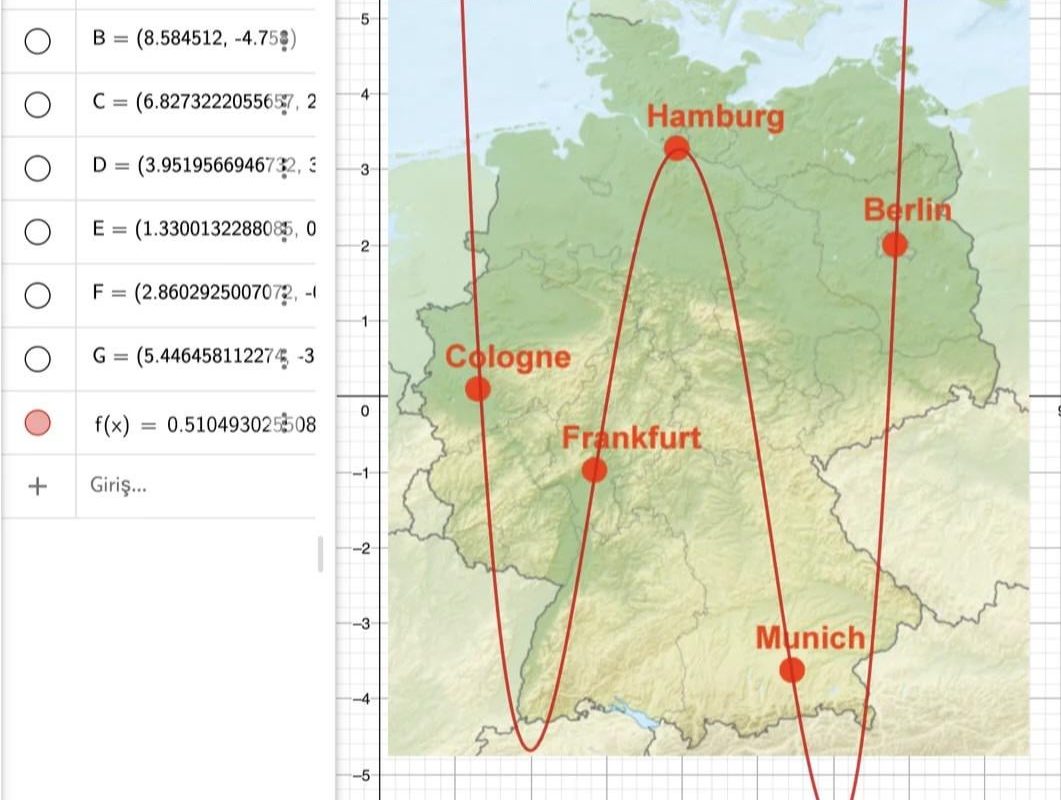
Germany’s 5 biggest cities lie perfectly on a 4th-degree polynomial.

Germany’s 5 biggest cities lie perfectly on a 4th-degree polynomial.

Title: Germany’s Top 5 Cities Align Perfectly on a 4th-Degree Polynomial Curve: Math Meets Geography!

Meta Description: Discover how Germany’s five largest cities—Berlin, Hamburg, Munich, Cologne, and Frankfurt—form a near-perfect 4th-degree polynomial curve. Explore the math behind this geographic marvel!

Introduction

Germany’s urban landscape is a tapestry of history, culture, and engineering. But did you know its five largest cities also form a striking mathematical pattern? When plotted geographically, Berlin, Hamburg, Munich, Cologne, and Frankfurt fall almost perfectly onto a 4th-degree polynomial curve. This quirky alignment has puzzled cartographers and math enthusiasts alike—blending geography with abstract algebra in an unexpected way.

In this article, we’ll break down this phenomenon, explore whether it’s a coincidence or a hidden secret of urban planning, and why polynomials might just hold the key to understanding Germany’s city distribution.

What Does the 4th-Degree Polynomial Curve Mean?

A 4th-degree polynomial is a mathematical function of the form:
[ f(x) = ax^4 + bx^3 + cx^2 + dx + e ]
When the latitudes and longitudes of Germany’s five biggest cities are plotted on a graph, they align closely with such a curve. While polynomials are often used in physics or economics, their role in mapping city locations is both surprising and delightful.

Germany’s Big 5: Cities Behind the Curve

Here are Germany’s five largest cities by population, which form this unique pattern:

1. Berlin (3.7M) – Capital and cultural heart.
2. Hamburg (1.9M) – Major port and gateway to the North Sea.
3. Munich (1.5M) – Bavaria’s economic powerhouse.
4. Cologne (1.1M) – Historic Rhine metropolis.
5. Frankfurt (760k) – Financial hub and transport nexus.

Plotting the Points:
If you map their coordinates (latitude vs. longitude), the curve bends northward through Hamburg and Berlin, dips toward Cologne/Frankfurt, and sweeps south to Munich.

Is This Alignment a Coincidence?

While the fit is uncanny, mathematicians note that any five points can be connected by a 4th-degree polynomial—a mathematical inevitability due to the “interpolation theorem.” This means:

• With 5 cities, a 4th-degree equation can always be found to pass through all points.
• The real question: Does this reveal anything meaningful about geography or history?

Possible Explanations:

1. Historical Trade Routes: Many German cities grew along rivers (Rhine, Elbe) and medieval trading paths, creating natural corridors.
2. Geographical Constraints: Mountain ranges (Alps to the south) and the North Sea may have indirectly shaped this distribution.
3. Urbanization Patterns: Industrialization favored clusters in resource-rich regions.

Why It’s Still Fascinating

Even if mathematically expected, the alignment highlights how math can model real-world patterns. Imagine applying this to:

• Urban Planning: Could future cities use polynomial models for infrastructure?
• Historical Analysis: Do other countries’ cities follow similar curves?
• Viral Maps: This trend sparked debates on Reddit and Twitter, proving math’s power to captivate!

Beyond Germany: A Global Pattern?

Germany isn’t alone! Similar experiments show:

• France’s top 5 cities (Paris, Marseille, Lyon, Toulouse, Nice) approximate a sine wave.
• Italy’s linear city layout (Milan to Naples) fits a 2nd-degree curve.
  However, these patterns rarely hold for more than five cities—reinforcing that small datasets create “perfect” but coincidental fits.

Final Thoughts: Math, Mystery, and German Geography

While Germany’s polynomial cities are more fun fact than urban secret, they remind us that math lurks everywhere—even in maps. Whether coincidence or coded genius, the blend of algebra and geography offers a fresh lens to explore the world.

Try It Yourself:
Grab coordinates from Google Maps, use a graphing tool (like Desmos or Python), and test if your country’s cities align on a polynomial curve!

Keywords: Germany cities, 4th-degree polynomial, urban planning mathematics, geographic patterns, German geography fun facts, math in maps.

Enjoyed this article? Share it with fellow geography and math enthusiasts, or explore our deep dives into how algorithms shape cities worldwide!